TERCEIRA QUANTIZAÇÃO PELO SDCTIE GRACELI

TRANS-QUÂNTICA SDCTIE GRACELI, TRANSCENDENTE, RELATIVISTA SDCTIE GRACELI, E TRANS-INDETERMINADA.

FUNDAMENTA-SE EM QUE TODA FORMA DE REALIDADE SE ENCONTRA EM TRANSFORMAÇÕES, INTERAÇÕES, TRANSIÇÕES DE ESTADOS [ESTADOS DE GRACELI], ENERGIAS E FENÔMENOS DENTRO DE UM SISTEMA DE DEZ OU MAIS DIMENSÕES DE GRACELI, E CATEGORIAS DE GRACELI.

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.  E DE ESTADOS TRANSICIONAIS =

TRANSFORMAÇÕES ⇔ INTERAÇÕES  ⇔  TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE  ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔  Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS,  ⇔   Δ MASSA ,   ⇔ Δ  CAMADAS ORBITAIS ,  ⇔  Δ FENÔMENOS  ,  ⇔  Δ  DINÂMICAS,   ⇔  Δ  VALÊNCIAS,   ⇔  Δ BANDAS,  Δ  entropia e de entalpia,  E OUTROS.  

x

 [EQUAÇÃO DE DIRAC].

 + FUNÇÃO TÉRMICA.

   +    FUNÇÃO DE RADIOATIVIDADE

  ,      +   FUNÇÃO DE TUNELAMENTO QUÂNTICO.

  + ENTROPIA REVERSÍVEL 

+      FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA

 ENERGIA DE PLANCK

X

• 
  V [R] [MA] =  Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......

  ΤDCG

  X

  Δe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......  =
  x
  

  sistema de dez dimensões de Graceli + 

  DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..
• 
  
• DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.
  

  x

  sistema de transições de estados, e estados  de Graceli, ESTADOS DE GRACELI TÉRMICOS E ESTADOS DOS ELEMENTOS QUÍMICO [ESTADOS ESPECÍFICOS DA MATÉRIA E ESTRUTURAS DE ELEMENTOS QUÍMICOS]

   fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].

número atômico, estrutura eletrônica, níveis de energia 

[comprimento de onda (λ).

onde c, velocidade da luz, é igual a .]

X

• TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI.
• X
• CATEGORIAS DE GRACELI
• T l    T l     E l       Fl         dfG l   

  N l    El                 tf l

  P l    Ml                 tfefel 

  Ta l   Rl

           Ll * D
        

X

 [ESTADO QUÂNTICO].

X

PARA TODO FORMA DE FUNÇÃO E EQUAÇÃO EM:

Em um sistema quântico constituído de muitas partículas idênticas com spin inteiro, a estatística de Bose-Einstein, ou estatística BE, é utilizada para descrever o sistema e calcular os valores médios das grandezas físicas.

Em um sistema de ${\displaystyle N}$ bósons idênticos de massa ${\displaystyle m}$, que possuem interação mútua desprezível, contidos em um recipiente de volume ${\displaystyle V}$, a uma temperatura ${\displaystyle T}$, em equilíbrio, o número médio de partículas ${\displaystyle {\bar {n}}_{s}}$ num estado de energia ${\displaystyle s}$ é dado por

${\displaystyle {\bar {n}}_{s}={\frac {g_{s}}{e^{\beta (\epsilon _{s}-\mu )}-1}}}$ ,

em que ${\displaystyle g_{s}}$ é a degenerescência quântica do estado ${\displaystyle s}$, ${\displaystyle \epsilon _{s}}$ é a energia do estado ${\displaystyle s}$, ${\displaystyle \mu }$ é o potencial químico, e ${\displaystyle \beta =1/k_{B}T}$, em que ${\displaystyle k_{B}}$ é a constante de Boltzmann^[1].

Índice

• 1Formulação matemática
• 2Gás de fótons
  • 2.1Radiação de corpo negro
• 3Comparação entre as estatísticas
• 4Condensação de Bose-Einstein
  • 4.1Temperatura crítica para um gás ideal de bósons
  • 4.2Hélio líquido
• 5Referências
• 6Bibliografia

Formulação matemática

Seja um gás de ${\displaystyle N}$ partículas idênticas confinadas em um volume ${\displaystyle V}$. Sendo ${\displaystyle Q_{i}}$ o conjunto das coordenadas generalizadas da i-ésima partícula e ${\displaystyle s_{i}}$ o índice rotulador dos possíveis estados quânticos desta única partícula, o estado do gás inteiro é então descrito pelo conjunto de números quânticos

${\displaystyle \{s_{1},s_{2},\dots ,s_{N}\}}$

os quais definem a função de onda ${\displaystyle \Psi }$ do gás nesse estado.

${\displaystyle \Psi =\Psi _{\{s_{1},s_{2},\dots ,s_{N}\}}(Q_{1},Q_{2},\dots ,Q_{N})}$

A estatística BE trata de partículas em que o spin total é medido em unidade inteiras de ${\displaystyle \hbar }$ — os chamados bósons — como, por exemplo, o átomo de Hélio-4 e o fóton.^[1] Partículas quânticas são indistinguíveis, ou seja, a troca de duas partículas não altera o estado do sistema. Além disto, a função de onda total para um sistema de bósons é simétrica sobre a troca de duas partículas^[1]

${\displaystyle \Psi (\dots ,Q_{i},\dots ,Q_{j})=\Psi (\dots ,Q_{j},\dots ,Q_{i})}$

Como consequência, os bósons não obedecem ao princípio de exclusão de Pauli, não havendo limitação no número de partículas que podem ocupar um dado estado quântico^[1]. Tomando este gás a uma temperatura ${\displaystyle T}$ e que cada partícula está em um estado ${\displaystyle r}$ de energia ${\displaystyle \epsilon _{r}}$ onde há ${\displaystyle n_{r}}$ partículas neste estado, o gás inteiro possui ${\displaystyle R}$ estados possíveis. Desprezando as interações mútuas entre as partículas, a energia do gás no estado ${\displaystyle R}$ será dada por

${\displaystyle E_{R}=n_{1}\epsilon _{1}+n_{2}\epsilon _{2}+\dots =\sum _{r}n_{r}\epsilon _{r}}$

em que a soma se estende sobre todos os estados ${\displaystyle r}$ possíveis de uma partícula^[2]. Como o número de partículas é fixo, também temos que

${\displaystyle \sum _{r}n_{r}=N}$

A função partição ${\displaystyle Z}$ do gás será dada por

${\displaystyle Z=\sum _{R}e^{-\beta E_{R}}=\sum _{R}e^{-\beta n_{1}\epsilon _{1}+\dots }}$

Essa soma é sobre todos os estados ${\displaystyle R}$ possíveis do gas inteiro, isto é, sobre todos os possíveis números ${\displaystyle n_{1},n_{2},n_{3},\dots }$^[2]. Como exp${\displaystyle [-\beta (n_{1}\epsilon _{1}+n_{2}\epsilon _{2}+...)]}$ é a probabilidade relativa de encontrar o gás em um estado partículas onde há ${\displaystyle n_{1}}$ partículas em 1, ${\displaystyle n_{2}}$ em partículas em 2 e assim sucessivamente, pode-se escrever o número médio de partículas em um estado ${\displaystyle s}$ como

${\displaystyle {\bar {n_{s}}}={\dfrac {\sum _{R}n_{s}e^{-\beta (n_{1}\epsilon _{1}+\dots )}}{\sum _{R}e^{-\beta (n_{1}\epsilon _{1}+\dots )}}}.}$

Somando todos os possíveis valores de ${\displaystyle n_{s}}$, usando a propriedade multiplicativa da exponencial e rearranjando, pode-se escrever ${\displaystyle {\bar {n_{s}}}}$ como

${\displaystyle {\bar {n_{s}}}={\dfrac {\displaystyle \sum _{n_{s}}n_{s}e^{-\beta n_{s}\epsilon _{s}}\cdot \sum _{n_{1},n_{2},\dots }^{(s)}e^{-\beta (n_{1}\epsilon _{1}+\dots )}}{\displaystyle \sum _{n_{s}}e^{-\beta n_{s}\epsilon _{s}}\cdot \sum _{n_{1},n_{2},\dots }^{(s)}e^{-\beta (n_{1}\epsilon _{1}+\dots )}}}}$

em que o sobrescrito ${\displaystyle (s)}$ no somatório indica a soma com exceção do estado ${\displaystyle s}$ em particular. Adotando a notação:

${\displaystyle \sum _{n_{1},n_{2},\dots }^{(s)}e^{-\beta (n_{1}\epsilon _{1}+\dots )}=Z_{s}(N)}$

A restrição de ${\displaystyle N}$ fixo implica que se uma partícula está no estado ${\displaystyle s}$, a soma ${\displaystyle \sum ^{(s)}}$ se estende pelas ${\displaystyle N-1,N-2,\dots }$ partículas restantes que podem ser colocadas nos estados ${\displaystyle n_{r}=1,2,3,\dots }$. Ao executar explicitamente a soma sobre ${\displaystyle {\bar {n_{s}}}}$ ter-se-á^[3]

${\displaystyle {\bar {n_{s}}}={\dfrac {0+e^{-\beta \epsilon _{s}}Z_{s}(N-1)+2e^{-2\beta \epsilon _{s}}Z_{s}(N-2)+\dots }{Z_{s}(N)+e^{-\beta \epsilon _{s}}Z_{s}(N-1)+2e^{-2\beta \epsilon _{s}}Z_{s}(N-2)+\dots }}}$

Estabelecendo a seguinte relação entre ${\displaystyle Z_{s}(N-\Delta N)}$ e ${\displaystyle Z_{s}(N)}$ onde ${\displaystyle N>>\Delta N}$

${\displaystyle \ln {Z_{s}(N-\Delta N)}=\ln {Z_{s}(N)}-{\dfrac {\partial \ln {Z_{s}}}{\partial N}}\cdot \Delta N=\ln {Z_{s}}-\alpha _{s}\Delta N}$

em que

${\displaystyle \alpha _{s}={\dfrac {\partial \ln {Z_{s}}}{\partial N}}}$

e portanto,

${\displaystyle Z_{s}(N-\Delta N)=Z_{s}(N)e^{-\alpha _{s}\Delta N}}$

Mas como ${\displaystyle Z_{s}(N)}$ é uma soma sobre muitos estados, espera-se que a variação de seu logaritmo natural com o número total de partícula seja imperceptível para o qual um estado particular ${\displaystyle s}$ seja omitido da soma^[3]. Vamos introduzir a aproximação de que ${\displaystyle \alpha _{s}}$ é independente de ${\displaystyle s}$, então podemos só escrever ${\displaystyle \alpha _{s}=\alpha }$ para todo ${\displaystyle s}$^[3]. Logo,

${\displaystyle \alpha ={\frac {\partial \ln {Z}}{\partial N}}}$

Do ensemble canônico, sabe-se que essa derivada parcial resulta em ${\displaystyle -\beta \mu }$, em que ${\displaystyle \mu }$ é o potencial químico do gás^[3]. Portanto,

${\displaystyle \alpha =-\beta \mu }$

Substituindo estes resultados em ${\displaystyle {\bar {n_{s}}}}$ teremos

${\displaystyle {\bar {n_{s}}}={\dfrac {e^{-\beta (\epsilon _{s}-\mu )}Z_{s}(N)+2e^{-2\beta (\epsilon _{s}-\mu )}Z_{s}(N)+\dots }{Z_{s}(N)+e^{-\beta (\epsilon _{s}-\mu )}Z_{s}(N)+2e^{-2\beta (\epsilon _{s}-\mu )}Z_{s}(N)+\dots }}}$

Cancelando ${\displaystyle Z_{s}(N)}$ ter-se-á

${\displaystyle {\bar {n_{s}}}={\dfrac {e^{-\beta (\epsilon _{s}-\mu )}+2e^{-2\beta (\epsilon _{s}-\mu )}+\dots }{1+e^{-\beta (\epsilon _{s}-\mu )}+2e^{-2\beta (\epsilon _{s}-\mu )}+\dots }}}$

Que é uma série geométrica. Usando a função partição de acordo com^[3] isso resultará em

${\displaystyle {\bar {n_{s}}}={\frac {1}{e^{\beta (\epsilon _{s}-\mu )}-1}}}$

Se o estado ${\displaystyle s}$ é degenerado com degenerescência ${\displaystyle g_{s}}$ então o número médio de partículas com energia ${\displaystyle \epsilon _{s}}$ é obtido multiplicando a expressão anterior por ${\displaystyle g_{s}}$. Finalmente,

${\displaystyle {\bar {n_{s}}}={\frac {g_{s}}{e^{\beta (\epsilon _{s}-\mu )}-1}}}$

A estatística de Bose-Einstein reduz-se à estatística de Maxwell-Boltzmann para energias: ${\displaystyle (\epsilon _{s}-\mu )>>kT}$^[4][5].

Gás de fótons

Um caso especial da estatística de Bose-Einstein é o gás de fótons. Fótons possuem spin inteiro igual a 1, então desta forma são considerados bósons. O caso é especial devido ao fato de que se considerarmos vários fótons dentro de um recipiente com volume V, o número destes fótons não será constante, pois conforme estes fótons interagem com as paredes do recipiente estes são absorvidos ou emitidos. Desta forma, não podemos impor um vínculo ao número total de fótons no sistema. Neste caso, precisaremos realizar as somas sobre todos os possíveis números de partículas em cada estado, da forma^[6]:

${\displaystyle n_{r}=0,1,2,3,...}$ para todo r.

A função partição para o gás de fótons é dada por:

${\displaystyle Z=\sum _{R}e^{-\beta (n_{1}\varepsilon _{1}+n_{2}\varepsilon _{2}+...)}}$

No qual R são todos os estados possíveis do gás. Como não há vínculos agora para o número de partículas por estado, podemos utilizar as propriedades das funções exponenciais e reescrever a soma acima como:

${\displaystyle Z=\sum _{n_{1},n_{2},...}e^{-\beta n_{1}\varepsilon _{1}}e^{-\beta n_{2}\varepsilon _{2}}...}$

Ou ainda:

${\displaystyle Z=\left(\sum _{n_{1}=0}^{\infty }e^{-\beta n_{1}\varepsilon _{1}}\right)\left(\sum _{n_{2}=0}^{^{\infty }}e^{-\beta n_{2}\varepsilon _{2}}\right)...}$

Como não há restrição para o número de fótons, as somas acima são consideradas até um número muito grande de partículas por estado de energia, no qual matematicamente isto se traduz a realizarmos a soma até o infinito, embora fisicamente, estejamos carregando a soma até um número muito grande de partículas. Como estamos tratando de uma exponencial com argumento negativo, após um certo valor os termos serão desprezíveis, não tendo problemas com divergências. Se olharmos com cuidado para as somas dentro dos colchetes acima, percebe-se que podemos escrevê-las como abaixo:

${\displaystyle \sum _{n_{1}=0}^{\infty }e^{-\beta n_{1}\varepsilon _{1}}=1+e^{-\beta \varepsilon _{1}}+e^{-2\beta \varepsilon _{1}}+...=\left({\frac {1}{1-e^{-\beta \varepsilon _{1}}}}\right)}$

Ou seja, cada termo é uma soma geométrica. Assim, podemos reescrever a função partição da seguinte forma:

${\displaystyle Z=\left({\frac {1}{1-e^{-\beta \varepsilon _{1}}}}\right)\left({\frac {1}{1-e^{-\beta \varepsilon _{2}}}}\right)...}$

E o logaritmo natural da função partição, que é o qual estamos interessados é dado por:

${\displaystyle \ln {Z}=-\sum _{r}\ln {(1-e^{-\beta \varepsilon _{r}})}}$

Nosso próximo objetivo agora é encontrar o número médio de partículas em um estado de energia ${\displaystyle \varepsilon _{s}}$. Tal resultado pode ser obtido através da expressão abaixo^[6]:

${\displaystyle {\bar {n_{s}}}=-{\frac {1}{\beta }}{\frac {\partial \ln {Z}}{\partial \varepsilon _{s}}}}$

Realizando a derivação do logaritmo natural da função partição, temos o resultado abaixo:

${\displaystyle {\bar {n_{s}}}={\frac {e^{-\beta \varepsilon _{s}}}{1-e^{-\beta \varepsilon _{s}}}}}$

O resultado acima é este pois a única derivada que não é zero é o termo da soma no qual ${\displaystyle r=s}$. Podemos simplificar o resultado acima, multiplicando e dividindo a expressão acima pela exponencial com o mesmo argumento, porém positivo, e assim obtemos o importante resultado dado por:

${\displaystyle {\bar {n_{s}}}={\frac {1}{e^{\beta \varepsilon _{s}-1}}}}$

Este resultado é conhecido como a distribuição de Planck, e fornece o número médio de fótons em um determinado estado s. Uma das aplicações mais famosas do resultado acima é no problema da radiação de corpo negro.

Radiação de corpo negro

Ver artigo principal: Radiação de corpo negro

Radiância espectral em função da frequência

Todo corpo a uma temperatura ${\displaystyle T}$ emite radiação eletromagnética. A distribuição de Planck fornece o espectro de emissão para uma classe especifica de corpos, os chamados corpos negros, definidos como os corpos que absorvem toda a radiação incidente. Pode-se modelar um corpo negro como uma cavidade metálica com volume ${\displaystyle V}$, tal que haja apenas um pequeno orifício em uma de suas paredes. Logo, esta cavidade absorve toda a radiação que entra por ali, e radiação emitida pelo orifício que é oriunda das emissões a partir das superfícies internas da cavidade se comporta como se fosse um corpo negro.^[7]

Busca-se a chamada radiância espectral ${\displaystyle R_{T}(f)df}$, que fornece a potência irradiada por unidade de área com frequência entre ${\displaystyle f}$ e ${\displaystyle f+df}$ pelo corpo estudado a uma data temperatura. Através de uma análise física do problema, pode-se mostrar que a radiância espectral está diretamente ligada com a densidade de energia dentro da cavidade. A relação entre as duas grandezas é dada por:

${\displaystyle R_{T}(f)={\frac {c}{4}}u_{T}(f)}$

Pode-se então obter a densidade de energia, e assim resolve-se o problema da mesma maneira. A densidade de energia pode ser obtida a partir da probabilidade de um nível com energia ${\displaystyle \varepsilon _{s}}$ estar ocupado por ${\displaystyle n_{s}}$ fótons, sendo assim se multiplicarmos este valor pelo número de médio fótons por unidade de volume naquele estado, teremos a densidade de energia dentro desta cavidade na forma:^[8]

${\displaystyle u_{T}(\varepsilon )={g(\varepsilon ){\bar {\varepsilon _{s}}}}}$

Onde ${\displaystyle g(\varepsilon )}$ é a densidade de estados ou degenerescência. Como temos o número médio de fótons em um estado ${\displaystyle s}$, basta multiplicar este número pela energia do estado ${\displaystyle s}$, assim:

${\displaystyle {\bar {\varepsilon _{s}}}={\frac {\varepsilon _{s}}{e^{\beta \varepsilon _{s}}-1}}}$

Como os estados do sistema estão muito próximos um dos outros, por conta da cavidade ocupar um volume V macroscópico, podemos tratar as variáveis como sendo contínuas. O número de estados por unidade de volume dentro da cavidade com frequência entre ${\displaystyle f}$ e ${\displaystyle f+df}$ é dada por:^[9]

${\displaystyle g(f)df={\frac {8\pi }{c^{3}}}f^{2}df}$

Sabemos que a energia e a frequência de um fóton estão ligado pela expressão de Planck ${\displaystyle E=hf}$, desta forma se fizermos a substituição sugerida, obtemos assim a expressão para a densidade de energia dentro de uma cavidade.

${\displaystyle u_{T}(f)={\frac {8\pi h}{c^{3}}}{\frac {f^{3}}{e^{\frac {hf}{kT}}-1}}}$

E a radiância espectral é dada diretamente por:

${\displaystyle R_{T}(f)={\frac {2\pi h}{c^{2}}}{\frac {f^{3}}{e^{\frac {hf}{kT}}-1}}}$

Todo o caminho feito para o obtenção do resultado foi a partir da análise das propriedades quânticas e estatísticas de fótons dentro de um volume V, e em equilíbrio térmico a uma temperatura T. Pode-se chegar no mesmo resultado analisando a interação da radiação eletromagnética dentro do volume V com as paredes do recipiente^[10].

Comparação entre as estatísticas

Comparação das distribuições de Maxwell-Boltzmann (MB), Bose-Einstein (BE) e Fermi-Dirac (FD).

Influência do potencial químico na distribuição BE.

Influência da temperatura na distribuição de BE.

Nota-se que um sistema de bósons possui uma maior ocupação dos estados, devido aos efeitos quânticos de simetria da função de onda do sistema ^[11]. Nesta distribuição identifica-se que para o regime ${\displaystyle (\epsilon -\mu )/kT>>1}$ as distribuições quânticas de Bose-Einstein (BE) e Fermi-Dirac (FD) se aproximam da distribuição clássica de Maxwell-Boltzmann (MB), que representa o regime de baixas densidades e altas temperaturas, ou seja, o limite clássico ^[12].

Em diferentes valores do potencial químico, nota-se que os estados de menor energia (próximos ao estado fundamental) são os mais populados. Para baixas temperaturas as partículas se concentram nos estados de menor energia. No limite de temperatura tendendo a zero, todas as partículas vão para o estado fundamental (${\displaystyle s=1}$), logo, ${\displaystyle {\bar {n}}_{1}\approx N}$ enquanto ${\displaystyle {\bar {n}}_{s}\approx 0}$ para os demais estados ^[13]. Já para altas temperaturas, devido à energia térmica do sistema, as partículas tem maior probabilidade de atingir estados mais energéticos.

Condensação de Bose-Einstein

O condensado de Bose-Einstein é uma fase da matéria formada por bósons a uma temperatura muito próxima do zero absoluto. Nestas condições, uma grande fração de átomos atinge o mais baixo estado quântico, e nestas condições os efeitos quânticos podem ser observados em escala macroscópica. Sistemas em baixa temperatura ou com densidade relativamente alta de partículas são mais prováveis de apresentarem comportamentos quânticos, mesmo em sistemas onde a interação intramolecular é desprezível^[14].

Temperatura crítica para um gás ideal de bósons

Um gás ideal de bósons não está sujeito ao princípio de exclusão de Pauli. Logo, os bósons podem se condensar no seu estado de menor energia. A densidade de estados ${\displaystyle g(\epsilon )}$ é dada por,

${\displaystyle g(\epsilon )={\frac {V}{4\pi ^{2}}}{\frac {(2m)^{\frac {3}{2}}}{\hbar ^{3}}}\epsilon ^{1/2}}$

Logo, o número de partículas ${\displaystyle N}$ pode ser reescrito como

${\displaystyle N=\int _{0}^{\infty }{\frac {g(\epsilon )}{e^{\beta (\epsilon -\mu )}-1}}d\epsilon }$

A distribuição continua pode ser utilizada pois os níveis do sistema quântico discreto são numerosos e estão muito próximos. Portanto,

${\displaystyle N={\frac {V}{4\pi ^{2}}}{\frac {(2m)^{\frac {3}{2}}}{\hbar ^{3}}}\int _{0}^{\infty }{\frac {\epsilon ^{1/2}}{e^{\beta (\epsilon -\mu )}-1}}d\epsilon }$

Porém, como a integração dar-se-á de ${\displaystyle \epsilon =0}$, a informação do estado fundamental é perdida. Todavia, quando a temperatura do sistema diminui, o potencial químico aumenta, e o número de partículas no estado fundamental é dada por ^[15]

${\displaystyle N_{0}={\frac {1}{e^{-\beta \mu }-1}}}$

Seja o número de partículas em estados excitados dado por ${\displaystyle N_{e}}$, temos

${\displaystyle N=N_{0}+N_{e}}$

${\displaystyle N={\frac {1}{e^{-\beta \mu }-1}}+{\frac {V}{4\pi ^{2}}}{\frac {(2m)^{\frac {3}{2}}}{\hbar ^{3}}}\int _{0}^{\infty }{\frac {\epsilon ^{1/2}}{e^{\beta (\epsilon -\mu )}-1}}d\epsilon }$

Porém, para temperaturas muito próximas de zero ${\displaystyle N\approx N_{0}}$, ou seja,

${\displaystyle N\approx {\frac {1}{e^{-{\frac {\mu }{kT}}}-1}}}$

Variação da temperatura de No/N (preto) e de Ne/N (vermelho) para uma gás ideal de bósons.

E, considerando ${\displaystyle N}$ grande,

${\displaystyle -{\frac {\mu }{kT}}\approx \ln \left(1+{\frac {1}{N}}\right)\approx {\frac {1}{N}}}$

Logo, ${\displaystyle e^{-\mu /kT}\approx 1}$. E ${\displaystyle N_{e}}$ se torna,

${\displaystyle N_{e}={\frac {V}{4\pi ^{2}}}{\frac {(2m)^{\frac {3}{2}}}{\hbar ^{3}}}\int _{0}^{\infty }{\frac {\epsilon ^{1/2}}{e^{\beta \epsilon }-1}}d\epsilon }$

Introduzindo a mudança de variável ${\displaystyle x=\beta \epsilon }$, temos

${\displaystyle N_{e}={\frac {2}{\sqrt {\pi }}}\left({\frac {2\pi mkT}{h^{2}}}\right)^{3/2}V\int _{0}^{\infty }{\frac {x^{1/2}}{e^{x}-1}}d\epsilon }$

A integral pode ser escrita em termos da função gama ${\displaystyle \Gamma (x)}$ e da função zeta de Riemann ${\displaystyle \zeta (x)}$. De fato, ela é igual a ${\displaystyle \Gamma (3/2)\zeta (3/2)}$, onde ${\displaystyle \Gamma (3/2)={\sqrt {\pi }}/2}$, logo,

${\displaystyle N_{e}=\zeta (3/2)V\left({\frac {2\pi mkT}{h^{2}}}\right)^{3/2}}$

A temperatura crítica, ou de Bose-Einstein, ${\displaystyle T_{c}}$, é a temperatura em que acima dela todos os bósons estão em um estado excitado, e pode ser encontrada tomando ${\displaystyle N=N_{e}}$, onde ${\displaystyle T=T_{c}}$, assim, da última equação,

${\displaystyle T_{c}={\frac {h^{2}}{2\pi mk}}\left[{\frac {N}{\zeta (3/2)V}}\right]^{2/3}}$

Se ${\displaystyle 0<T<T_{c}}$, a razão de bósons no estado excitado em relação ao total, é

${\displaystyle {\frac {N_{e}}{N}}=\left({\frac {T}{T_{c}}}\right)^{3/2}}$

Consequentemente, a razão para os bósons no estado fundamental é,

${\displaystyle {\frac {N_{0}}{N}}=1-\left({\frac {T}{T_{c}}}\right)^{3/2}}$

Em mecânica estatística, a estatística Maxwell–Boltzmann descreve a distribuição estatística de partículas materiais em vários estados de energia em equilíbrio térmico, quando a temperatura é alta o suficiente e a densidade é baixa suficiente para tornar os efeitos quânticos negligenciáveis. A estatística Maxwell–Boltzmann é consequentemente aplicável a quase qualquer fenômeno terrestre para os quais a temperatura está acima de poucas dezenas de kelvins.^[1][2]

O número esperado de partículas com energia ${\displaystyle \epsilon _{i}}$ para a estatística de Maxwell–Boltzmann é ${\displaystyle N_{i}}$ onde:

${\displaystyle {\frac {N_{i}}{N}}={\frac {g_{i}}{e^{(\epsilon _{i}-\mu )/kT}}}={\frac {g_{i}e^{-\epsilon _{i}/kT}}{Z}}}$

onde:

• ${\displaystyle N_{i}}$ é o número de partículas no estado i
• ${\displaystyle \epsilon _{i}}$ é a energia do estado i-ésimo
• ${\displaystyle g_{i}}$ é a degenerescência do nível de energia i, o número de estados dos partículas (excluindo o estado de "partícula livre") com energia ${\displaystyle \epsilon _{i}}$
• ${\displaystyle \mu }$ é o potencial químico
• ${\displaystyle k}$ é a constante de Boltzmann
• ${\displaystyle T}$ é a temperatura absoluta
• ${\displaystyle N}$ é o número total de partículas

${\displaystyle N=\sum _{i}N_{i}\,}$

• ${\displaystyle Z}$ é a função partição

${\displaystyle Z=\sum _{i}g_{i}e^{-\epsilon _{i}/kT}}$

• ${\displaystyle e^{(...)}}$ é a função exponencial, sendo e o número de Euler

A distribuição de Maxwell-Boltzmann tem sido aplicada especialmente à teoria cinética dos gases, e outros sistemas físicos, além de em econofísica para predizer a distribuição da renda. Na realidade a distribuição de Maxwell-Boltzmann é aplicável a qualquer sistema formado por N "partículas" ou "indivíduos" que interacambiam estacionariamente entre si uma certa magnitude ${\displaystyle m}$ e cada um deles têm uma quantidade ${\displaystyle m_{i}}$ da magnitude ${\displaystyle m}$ e ao longo do tempo ocorre que ${\displaystyle \sum _{i=1}^{N}M=m_{1}+m_{2}+...+m_{N}}$.

L

A Energia de Fermi é a energia do nível ocupado mais energético em um sistema quântico fermiônico à temperatura de zero absoluto. A definição estende-se também a sistemas acima do zero absoluto, caso em que a energia de fermi corresponde à energia obtida mediante uma média das energias dos níveis quânticos com probabilidade de ocupação - devido à agitação térmica - diferentes da unidade, cada qual ponderado pela respectiva probabilidade de ocupação. Associa-se via de regra à energia de fermi a notação E_F, e a nomenclatura retrata nítida homenagem ao físico ítalo-americano Enrico Fermi.

Índice

• 1Introdução
  • 1.1Contexto geral
  • 1.2Contexto avançado
• 2Ilustração do conceito para compartimento monodimensional quadrado
• 3O caso tridimensional
• 4Energias de Fermi típicas
  • 4.1Anãs brancas
  • 4.2Núcleos
• 5Nível de Fermi
• 6Referências
• 7Bibliografia
• 8Ver também

Introdução

Contexto geral

A energia de Fermi é importante na hora de entender o comportamento de partículas fermiônicas, como por exemplo os elétrons. Os férmions são partículas de spin semi-inteiro para as quais verifica-se a validade do princípio de exclusão de Pauli - que dita que dois férmions idênticos não podem ocupar simultaneamente o mesmo estado quântico. Desta maneira, quando um sistema possui vários elétrons, estes ocuparão níveis de energia maiores a medida que os níveis inferiores estejam preenchidos.

A energia de Fermi é um conceito que tem muitas aplicações na teoria dos orbitais atômicos, no comportamento dos semicondutores e na física do estado sólido em geral.

Em física do estado sólido a superficie de Fermi é a superficie no espaço de momentos na qual a energia de excitação total se iguala à energia de Fermi. Esta superfície pode ter uma topologia não trivial. Simplificadamente se pode dizer que a superfície de Fermi divide os estados electrônicos ocupados dos que permanecem livres.

Enrico Fermi e Paul Dirac, derivaram as estatísticas de Fermi-Dirac. Estas estatísticas permitem predizer o comportamento de sistemas formados por um grande número de elétrons, especialmente em corpos sólidos.

A energia de Fermi de um gás de Fermi (ou gás de elétrons livres) não relativista tridimensional se pode relacionar com o potencial químico através da equação:

${\displaystyle \mu =\epsilon _{F}\left[1-{\frac {\pi ^{2}}{12}}\left({\frac {kT}{\epsilon _{F}}}\right)^{2}+{\frac {\pi ^{4}}{80}}\left({\frac {kT}{\epsilon _{F}}}\right)^{4}+...\right]}$

onde ε_F é a energia de Fermi, k é a constante de Boltzmann e T é a temperatura. Portanto, o potencial químico é aproximadamente igual a a energia de Fermi à temperaturas muito inferiores a uma energia característica denominada Temperatura de Fermi, ε_F/k. Esta temperatura característica é da ordem de 10⁵K para um metal a uma temperatura ambiente de (300 K), pelo que a energia de Fermi e o potencial químico são essencialmente equivalentes. Este é um detalhe significativo dado que o potencial químico, e não a energia de Fermi, é quem aparece nas estatísticas de Fermi-Dirac.

Contexto avançado

Principais energias em estrutura de bandas para sólidos cristalinos.

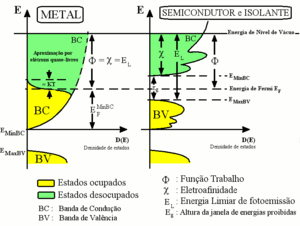
Elétrons são férmions, ou seja, são partículas regidas pela estatística de Fermi. Nesta estatística, um dado estado quântico pode ser ocupado por no máximo um e não mais que um férmion, e portanto a máxima probabilidade de ocupação de um dado estado quântico é um. Os elétrons situados dentro da amostra estão confinados por um potencial atrativo exercido pelos íons positivos da rede. Conforme mostrado pela mecânica quântica, potenciais confinantes apresentam níveis de energias discretos. No caso dos átomos isto se reflete nos tão conhecidos níveis atômicos de energia e no caso dos sólidos cristalinos, a aproximação entre os átomos leva a um agrupamento dos estados em bandas de energia. Estas bandas são vistas nas relações de dispersão para os sólidos como sendo as regiões de energia permitidas para os elétrons, separadas umas das outras por janelas de energias proibidas (ou “gaps”).

Rigorosamente falando,^[1] a energia do nível de Fermi é definida em sistemas à temperatura de zero absoluto. Nesse caso, a energia do nível de Fermi é a energia do nível mais energético ocupado, visto que nessa temperatura todos os níveis com energia menor que a energia do nível de Fermi estariam ocupados (probabilidade igual a 1) e todos os níveis com energia acima, desocupados (probabilidade de ocupação nula). Para sistemas em temperaturas não nulas, não temos mais uma transição abrupta da probabilidade de ocupação, e sim uma probabilidade dada pela distribuição de Fermi-Dirac. Considera-se então como a energia do nível de Fermi a energia obtida pela média aritmética ponderada das energias de cada estado energético afetado pela excitação térmica (estados com probabilidades de ocupação diferentes de 1 ou 0) pesadas cada qual pela respectiva probabilidade de ocupação do estado associado. O denominador desta média será obviamente o número de estados envolvidos no processo. Repare que em acordo com a estatística de Fermi, dentre os referidos estados os menos energéticos têm probabilidade de ocupação maior do que aqueles mais energéticos. Para aproximação de elétrons livres a densidade de estados cresce com a raiz quadrada da energia, resultando em uma parábola no gráfico de energia x densidade de estados. Em semicondutores e isolantes esta dependência pode ser bem mais complicada.

Outra definição equivalente implica dizer que a energia de Fermi corresponde ao potencial eletroquímico do sistema na temperatura de zero absoluto. Uma extensão a temperaturas maiores é evidente, e a energia de Fermi corresponde assim ao potencial eletroquímico do sistema na temperatura considerada. A energia de Fermi expressa, portanto, qual seria a variação da energia interna total do sólido, considerado sempre como sistema isolado e em equilíbrio termodinâmico, caso um elétron fosse dele removido. Sendo E_N^total a energia total do sistema no estado neutro, em seu equilíbrio termodinâmico, e E_N-1^total a energia total do sistema também em seu novo equilíbrio termodinâmico mas após a remoção do elétron, temos que:

E_F = E_N^total - E_N-1^total

Nas definições acima, o nível de referência é o nível de menor energia disponível aos N elétrons, e a remoção de um elétron provoca, então, a redução da energia do sistema. Neste referencial a energia de Fermi é, portanto, positiva, bem como o potencial eletroquímico.

Quando dois materiais diferentes são colocados em contato, a condição de equilíbrio termodinâmico exige que as suas energias de Fermi sejam iguais. Se as energias de Fermi fossem diferentes, a passagem de um elétron do sólido com maior energia de Fermi para o sólido com menor energia de Fermi resultaria em uma diminuição da energia total do sistema e o sistema composto não estaria, então, em sua configuração de equilíbrio, a de mínima energia, conforme exigido pelas leis da termodinâmica. Este fato dá origem a um fenômeno conhecido por diferença de potencial de contato que encontra diversas aplicações práticas, a saber na eletrônica de estado sólido (junção PN) e no uso do metal de sacrifício em navios.

Ilustração do conceito para compartimento monodimensional quadrado

A monodimensional compartimento quadrado infinito é um modelo para uma caixa mono dimensional. É um sitema modelo padrão em mecânica quântica para o qual a solução para uma partícula isolada é bem conhecido. Os níveis são marcados por um único número quântico n e as energias são dadas por

${\displaystyle E_{n}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n^{2}\,}$.

Suponha-se agora que em vez de uma partícula nesta caixa nós temos N partículas na caixa e que estas partículas são férmions com spin 1/2. Então somente duas partículas podem ter a mesma energia i.e. duas partículas podem ter a energia de ${\displaystyle E_{1}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}}$, ou duas partículas podem ter energia ${\displaystyle E_{2}=4E_{1}}$ e assim por diante. A razão que duas partículas podem ter a mesma energia é que uma partícula de spin 1/2 pode ter um spin de 1/2 (spin "acima") ou um spin de -1/2 (spin "abaixo"), conduzindo a dois estadois para cada nível de energia. Quando nós olhamos na energia total deste sistema, a configuração para as quais a energia total é a menor (o estado fundamental), é a configuração onde todos os níveis de energia acima de n=N/2 estão ocupados e todos os níveis mais altos estão vazios. A energia de Fermi é consequentemente

${\displaystyle E_{f}=E_{N/2}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}(N/2)^{2}\,}$.

O caso tridimensional

O caso tridimensional isotrópico é conhecido como a esfera de Fermi.

Deixe-nos agora considerar uma caixa cúbica tridimensional que tem um lado de comprimento L (ver compartimento quadrado infinito). Este torna-se uma muito boa aproximação para descrever elétrons em um metal.

Os estados agora são marcados po três números quânticos n_x, n_y, e n_z. As energias da partícula isolada são

${\displaystyle E_{n_{x},n_{y},n_{z}}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left(n_{x}^{2}+n_{y}^{2}+n_{z}^{2}\right)\,}$

n_x, n_y, n_z são inteiros positivos.

Existem múltiplos estados com a mesma energia, por exemplo ${\displaystyle E_{100}=E_{010}=E_{001}}$. Agora deixemos colocar-se N férmions não interativos de spin 1/2 nesta caixa. Para calcular a energia de Fermi, nós veremos no caso de que N é grande.

Se nós introduzios um vetor ${\displaystyle {\vec {n}}=\{n_{x},n_{y},n_{z}\}}$ então cada estado quântico corresponde a um ponto num "n-espaço" com energia

${\displaystyle E_{\vec {n}}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}|{\vec {n}}|^{2}\,}$.

O número de estados com energia menor que E_f é igual ao número de estados que residem em uma esfera de raio ${\displaystyle |{\vec {n}}_{f}|}$ na região do "n-espaço" onde n_x, n_y, n_z são positivos. No estado básico este número iguala o número de férmions no sistema.

${\displaystyle N=2\times {\frac {1}{8}}\times {\frac {4}{3}}\pi n_{f}^{3}\,}$

Os três férmions que ocupam os mais baixos estados de energia formam uma esfera em espaço de momento. A superfície desta esfera é a superfície de Fermi.

o fator é de dois é novamente porque são doisestados de spin, o fator de 1/8 é porque somente 1/8 da esfera repousa na região onde todos n são positivos.

Nós obtemos

${\displaystyle n_{f}=\left({\frac {3N}{\pi }}\right)^{1/3}}$

então a energia de Fermi é dada por

${\displaystyle E_{f}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n_{f}^{2}}$

${\displaystyle ={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N}{\pi }}\right)^{2/3}}$

Tais resultados em uma relação entre a energia de Fermi e o número de partículas por volume (quando nós substituímos L² com V^2/3):

${\displaystyle E_{f}={\frac {\hbar ^{2}}{2m}}\left({\frac {3\pi ^{2}N}{V}}\right)^{2/3}\,}$

A energia de Fermi total de um esfera de fermi de ${\displaystyle N_{0}}$ férmions é dada por

${\displaystyle E_{t}={\int _{0}}^{N_{0}}E_{f}(N)dN={3 \over 5}N_{0}E_{f}}$

${\displaystyle E_{t}={\int _{0}}^{N_{0}}E_{f}(N)dN={\int _{0}}^{N_{0}}{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N}{\pi }}\right)^{\frac {2}{3}}dN}$

${\displaystyle ={\frac {3^{\frac {2}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{2mL^{2}}}{\int _{0}}^{N_{0}}N^{\frac {2}{3}}dN={\frac {3^{\frac {2}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{2mL^{2}}}\left({\frac {3}{5}}N_{0}^{\frac {5}{3}}\right)={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{10mL^{2}}}N_{0}^{\frac {5}{3}}}$

Energia de Fermi total:

${\displaystyle E_{t}={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{10mL^{2}}}N_{0}^{\frac {5}{3}}}$

Integração por substituição:

${\displaystyle E_{t}={\frac {3}{5}}N_{0}E_{f}={\frac {3}{5}}N_{0}\left[{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N_{0}}{\pi }}\right)^{2/3}\right]={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{10mL^{2}}}N_{0}^{\frac {5}{3}}}$

${\displaystyle E_{t}={\frac {3}{5}}N_{0}E_{f}}$

A eliminação de ${\displaystyle L}$ em favor de ${\displaystyle V}$:

${\displaystyle L^{2}=V^{\frac {2}{3}}}$

${\displaystyle E_{t}={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}N_{0}^{\frac {5}{3}}}{10mV_{0}^{\frac {2}{3}}}}}$

Energias de Fermi típicas

Anãs brancas

Estrelas conhecidas como anãs brancas tem massa comparável a nosso Sol, mas têm um raio aproximadamente 100 vezes menor. As alta densidades implicam que os elétrons estão não mais ligados a um núcleo isolado e formam um gás de elétrons degenerado. Os números da densidade de elétrons em uma anã branca são da ordem de 10³⁶ elétrons/m³. Isto significa que sua energia de Fermi é:

${\displaystyle E_{f}={\frac {\hbar ^{2}}{2m_{e}}}\left({\frac {3\pi ^{2}(10^{36})}{1\ \mathrm {m} ^{3}}}\right)^{2/3}\approx 3\times 10^{5}\ \mathrm {eV} \,}$

Núcleos

Outro exemplo típico é as partículas em um núcleo de um átomo. Os núcleons de um núcleo atômico pode ser tratado, assim, como um gás de Fermi e como tal, modelado.^[2]

O raio do núcleo é aproximadamente^[3]:

${\displaystyle R=\left(1.25\times 10^{-15}\mathrm {m} \right)\times A^{1/3}}$

onde A é o número de núcleons.

O número densidade de núcleons em um núcleo é conseqüentemente:

${\displaystyle n={\frac {A}{{\begin{matrix}{\frac {4}{3}}\end{matrix}}\pi R^{3}}}\approx 1.2\times 10^{44}\ \mathrm {m} ^{-3}}$

Agora, como a energia de fermi somente aplica-se a férmions de mesmo tipo, deve-se dividir esta energia por dois. Isto por causa da presença de nêutrons que não afetam a energia de Fermi dos prótons no núcleo, e vice versa.^[4][5][6]

Assim a energia de fermi de um núcleo é dada por:

${\displaystyle E_{f}={\frac {\hbar ^{2}}{2m_{p}}}\left({\frac {3\pi ^{2}(6\times 10^{43})}{1\ \mathrm {m} ^{3}}}\right)^{2/3}\approx 30\times 10^{6}\ \mathrm {eV} =30\ \mathrm {MeV} }$

O raio do núcleo admite desvios em torno do valor mencionado acima, então um típico valor para a energia de Fermi normalmente dada é 38 MeV.

Um gás de férmions, gás de Fermi ou gás de elétrons livres é um conjunto de férmions não interativos. É a versão na Mecânica Quântica de um gás ideal, para o caso de partículas fermiônicas. Elétrons em metais e semicondutores e nêutrons em estrelas de nêutrons podem aproximadamente ser considerados gases de Fermi.

A distribuição de energia dos férmions em um gás de Fermi em equilíbrio térmico é determinada por sua densidade, pela temperatura e pelos estados de energia disponíveis, via a estatística de Fermi-Dirac. Pelo princípio de exclusão de Pauli, nenhum estado quântico pode ser ocupado por mais que um férmion, então a energia total do gás de Fermi à temperatura do zero absoluto é tão grande quanto o produto do número de partículas pelo estado de energia de cada partícula. Por esta razão, a pressão de um gás Fermi é diferente de zero na temperatura de zero absoluto, em contraste com um gás ideal clássico. Esta então chamada pressão de degenerescência estabiliza uma estrela de nêutrons (um gás de Fermi de nêutrons) ou uma estrela anã branca (um gás de Fermi de elétrons) contra a tração interna da gravidade.

É possível definir uma temperatura de Fermi abaixo do qual o gás pode ser considerado degenerado. Esta temperatura depende da massa dos férmions e da energia da densidade dos estados. Para metais, a temperatura do gás de elétrons de Fermi é geralmente de muitos milhares de kelvins, quando então eles podem ser considerados degenerados. A máxima energia dos férmions a temperatura do zero absoluto é chamada energia de Fermi. A superfície da energia de Fermi no momento espacial é chamada superfície de Fermi.

Desde que as interações são negligenciadas por definição, o problema de tratar propriedades do equilíbrio e o comportamento dinâmico de um gás de Fermi se reduz ao estudo do comportamento de partículas independentes e isoladas. Como está, é ainda relativamente tratável e dá forma ao ponto de servir de base para teorias mais avançadas (tais como a teoria do líquido de Fermi ou a teoria perturbacional) as quais levam em conta as interações com algum grau de exatidão.

Índice

• 1Descrição matemática
• 2Gás de Fermi como modelo para os núcleos dos átomos
• 3Referências
• 4Ver também
• 5Ligações externas

Descrição matemática

Dentro da estrutura que a física estatística possibilita, segue-se que com a ajuda de conjuntos estatísticos para um número médio de ocupação ${\displaystyle \langle n_{i}\rangle }$ dos estados ${\displaystyle |i\rangle }$ com a energia ${\displaystyle E_{i}}$ da estatística de Fermi-Dirac:

${\displaystyle \langle n_{i}\rangle ={\frac {1}{e^{\frac {E_{i}-\mu }{k_{B}T}}+1}}}$

Onde ${\displaystyle \mu }$ é o potencial químico, ${\displaystyle T}$ a temperatura e ${\displaystyle k_{B}}$ a constante de Boltzmann.

Estes férmions, que estão sujeitos ao princípio de exclusão de Pauli, podem estar na condição de máxima ocupação, ou seja ${\displaystyle \langle n_{i}\rangle \leq 1}$. Esta condição é que a estatística de Fermi-Dirac tratará para qualquer valor de preenchimento pleno ${\displaystyle \mu }$, porque o potencial químico de um gás ideal de Fermi não é sujeito a quaisquer restrições.